2.2. Por tres cuadrantes
Recta oblicua.
Toda recta oblicua a los dos planos de proyección, excepto la que pasa por la línea de tierra, corta a ambos planos, por tanto, pasará por tres cuadrantes.
En la animación inferior te mostramos cómo determinar las trazas y proyecciones de una recta oblicua, así como los cuadrantes por los que pasa; en este caso por el primero, cuarto y tercero.
Recta de perfil.
En el caso particular de la recta de perfil, como ya vimos en el tema anterior, para determinar sus trazas normalmente debemos recurrir a la proyección auxiliar de perfil, lo que también nos indicará los cuadrantes por los que pasa.
En la siguiente animación puedes ver cómo se determinan las trazas y los cuadrantes por lo que pasa; observa cómo se ha calculado la intersección de dicha recta con los planos bisectores.
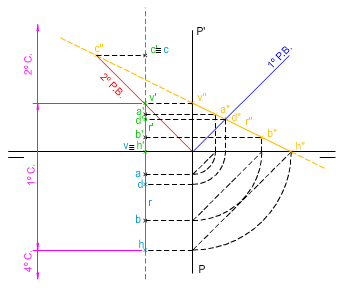 |
En la imagen izquierda puedes ver cómo se han determinado las trazas de una recta de perfil, conocidas las proyecciones de dos de sus puntos (A y B), así como la intersección de dicha recta con el primer plano bisector. Te pedimos que: a) Determines dichas trazas. b) El punto D intersección con el primer plano bisector. c) Los cuadrantes por los que pasa la recta dada. |