3.2. Hipérbola
Aplicando potencia determinamos los centros de circunferencias tangentes (interior y exterior) a la focal de la hipérbola que pasando por el otro foco pertenezcan a la recta intersección.
Punto de interesección con una recta. En la animación inferior te mostramos cómo se determinan los puntos intersección de una recta con una hipérbola, conocidos los siguientes elementos: parámetros 2a y 2c y la recta M.
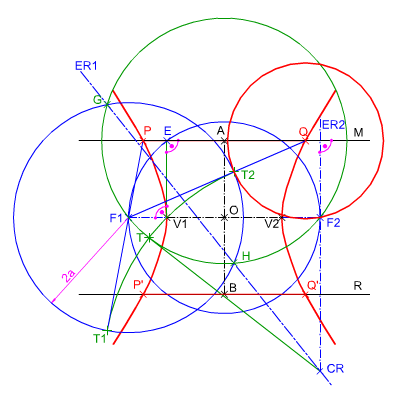 |
En la figura de la izquierda puedes ver cómo se han determinado los puntos intersección P y Q y sus simétricos de dos rectas paralelas M y R con una Hipérbola. Para poder resolver este ejercicio debes repasar las nociones aprendidas sobre la Hipérbola en el tema anterior, y aplicar los conceptos y procedimientos explicados en este apartado y los anteriores. Datos: ejes mayor y menor y las dos rectas paralelas. Material necesario:
|