1.3. Hipérbola
Definición.
La Hipérbola es una curva abierta, plana y con dos ramas, cuyos puntos tiene una distancia constante a los focos igual a la diferencia a de las distancias de un punto cualquiera de la hipérbola respecto a ellos.
Tiene los mismos elementos que la Elipse: dos ejes de simetría perpendiculares entre sí; el Eje mayor (2a) determinado por los vértices de la hipérbola, el eje menor (imaginario)es perpendicular al mayor en su punto medio (es su mediatriz) que es el centro de la curva.
La Hipérbola es una curva abierta, plana y con dos ramas, cuyos puntos tiene una distancia constante a los focos igual a la diferencia a de las distancias de un punto cualquiera de la hipérbola respecto a ellos.
Tiene los mismos elementos que la Elipse: dos ejes de simetría perpendiculares entre sí; el Eje mayor (2a) determinado por los vértices de la hipérbola, el eje menor (imaginario)es perpendicular al mayor en su punto medio (es su mediatriz) que es el centro de la curva.
Elementos.
Como en el caso de la Elipse, los elementos de la Hipérbola son todos los que podemos encontrar en una curva cónica, aunque uno de ellos (el eje menor) no desempeñe el mismo papel que en la Elipse.En la animación inferior puedes ver los elementos y propiedades de la Hipérbola, para ello debes colocar el cursor en las líneas y caracteres que aparecen y luego pulsar el botón izquierdo de tu ratón.
Hipérbola equilátera.
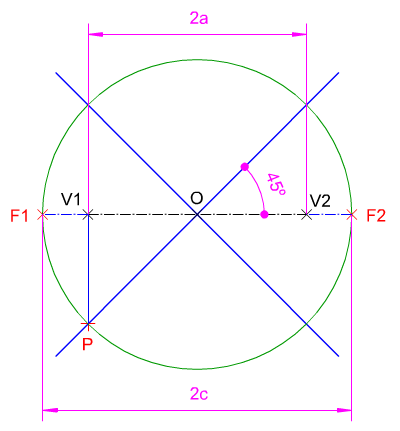
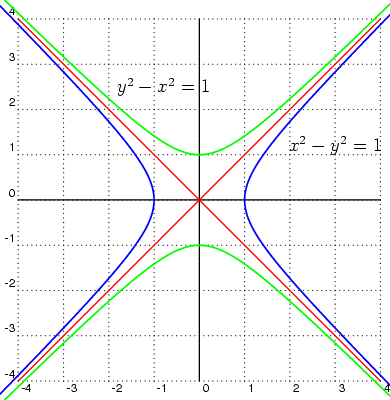 Las hipérbolas equiláteras se emplean en la ecuación de los gases nobles.
Las hipérbolas equiláteras se emplean en la ecuación de los gases nobles.
Para que una hipérbola sea equilátera sus asíntotas deben ser perpendiculares entre sí, por tanto, cada una de ellas formará un ángulo de 45º con el eje mayor de simetría de dicha curva cónica.
En la imagen izquierda (archivo de Wikimedia Commons, un depósito de contenido libre hospedado por la Fundación Wikimedia) te mostramos la representación de una Hipérbola equilátera.
Determinar elementos: para poder determinar los parámetros de una Hipérbola necesitaremos como mínimo dos datos. En las siguientes animaciones te mostramos cómo determinar distintos elementos a partir de los parámetros 2a y 2c.
- El eje de simetría menor.
- Las asintotas.
Ángulo del plano sección e hipérbola.
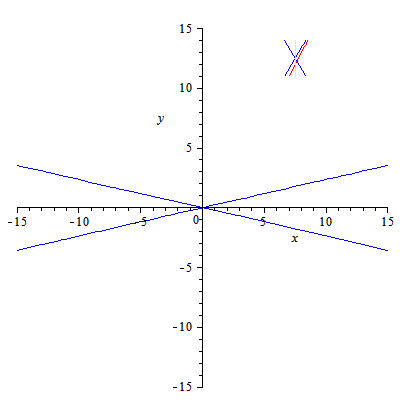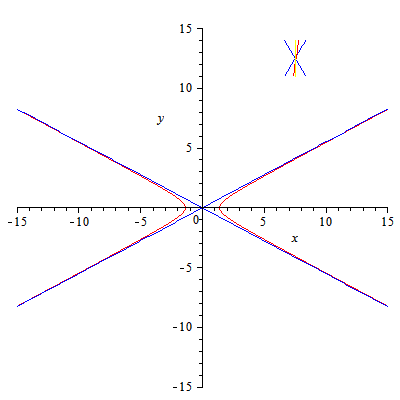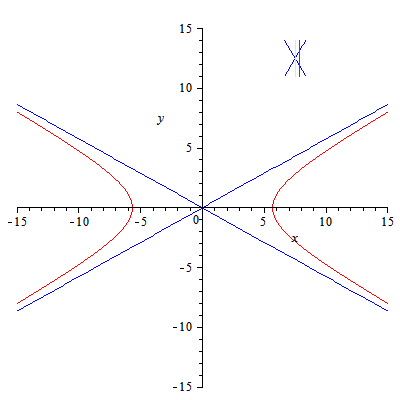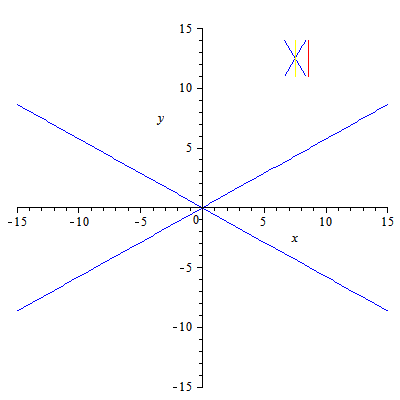 En la imagen de la izquierda (archivo de Wikimedia Commons, un depósito de contenido libre hospedado por la Fundación Wikimedia) te mostramos cómo cambia el ángulo de las ramas de una Hipérbola según sea el ángulo que forme el plano sección con el eje del cono recto de revolución.
En la imagen de la izquierda (archivo de Wikimedia Commons, un depósito de contenido libre hospedado por la Fundación Wikimedia) te mostramos cómo cambia el ángulo de las ramas de una Hipérbola según sea el ángulo que forme el plano sección con el eje del cono recto de revolución.
 |
Para resolverlo debes de aplicar los conceptos y procedimientos explicados en este apartado.
|