2.2. Rectas y circunferencias

Icono IDevice Actividad
Recuerda que el eje radical de dos circunferencias tangentes es la recta tangente a ambas.

Circunferencias tangentes a una recta y a otra circunferencia dadas, conocido el punto de tangencia en la curva

Por el punto de tangencia de la circunferencia dada pasará un eje radical (recta tangente), el otro eje radical es la recta tangente s la recta dada (tangente a la circunferencia solución) y contendrá al centro radical.

 


 

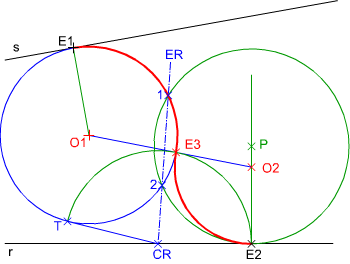
Circunferencias tangentes a una recta y a otra circunferencia dadas, conocido el punto de tangencia en la recta.

Como en el ejercicio anterior debemos detererminar el centro radical, para ello trazamos por el punto de tangencia de la recta dada una circunferencia tangente que al cortar a la otra dada determinará un eje radical, el otro eje radical es la recta dada (tangente a la circunferencia solución) y contendrá al centro radical.

 


 

Icono de iDevice Caso de estudio

Enlazar mediante arcos tangentes dos rectas concurrentes de vértice inaccesible.


En la imagen de la izquierda puedes ver cómo mediante dos circunferencia tangentes entre sí se han enlazado dos rectas concurrentes, que se cortan fuera del dibujo.

En el curso anterior resolvimos este ejercicio mediante métodos complejos.
Si aplicamos potencia simplificaremos el trazado.

Para resolverlo debes de aplicar el primer método explicado en este apartado.

Material necesario:

  • Lápiz blando y duro.
  • Compás.
  • Plantilla de dibujo (escuadra y cartabón).
  • Hojas para realizar trazados de prueba. 
 Para realizar este ejercicio debes descargar este documento pdf. 

« Anterior | Siguiente »