Circunferencias tangentes a una recta y que pasen por dos puntos.

Para realizar este ejercicio debemos determinar el centro radical.
Como las circunferencias solución serán secantes entre sí un eje radical pasará por los puntos de intersección, el otro eje radical es la recta tangente y contendrá al centro radical.

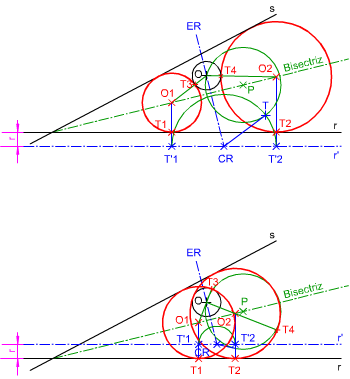
Circunferencias tangentes a dos rectas y que pasen por un punto.

Como en el ejercicio anterior debemos determinar el centro radical.
Dado que las dos rectas son concurrentes el centro de las circunferencias solución estará situado en su bisectriz.
Dichas circunferencias serán secantes por el punto dado, luego un eje radical pasará por él perpendicularmente a la bisectriz, el otro eje radical es la recta tangente y contendrá al centro radical.