3.1. Triángulos y cuadriláteros
Comenzamos el estudio de las formas planas más sencillas: triángulos y
cuadriláteros paralelogramos, estos últimos constituyen la base sobre la que
trazaremos cualquier forma plana.
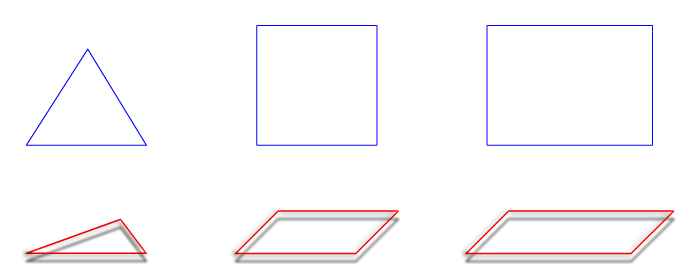
En la imagen superior tienes un ejemplo de perspectiva caballera de un
triángulo equilátero, un cuadrado y un rectángulo.
La perspectiva caballera de un triángulo la podemos realizar a partir de las coordenadas de sus vértices; o podemos optar por inscribirlo dentro de un paralelogramo, cuadrado o rectángulo.
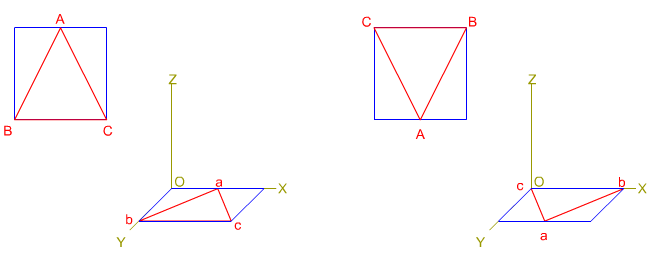
En la imagen inferior tienes dos ejemplos de perspectiva caballera de un triángulo equilátero, en un caso uno de los lados del triángulo es paralelo a un eje del sistema y en el otro está contenido en él.
PERSPECTIVA CABALLERA DE UN CUADRADO.
En la representación de cuadriláteros paralelogramos siempre los consideraremos con sus lados dispuestos de forma paralela a los ejes del sistema. En caso contrario tendremos que inscribirlo en otro paralelogramo.
Si tenemos que representar un romo, romboide o cualquier cuadrilátero no paralelogramo (trapecios y trapezoides) lo inscribiremos en un paralelogramo cuadrado o rectángulo.
En la animación inferior puedes ver la perspectiva caballera de un cuadrado: dos de sus lados están contenidos en los ejes axonométricos, y los otros dos son lados paralelos a dichos ejes.
Perspectiva caballera de un rombo.
En la siguiente animación puedes los pasos a seguir para trazar la perspectiva caballera de un rombo. Datos: ángulo XY 45º y C.R. 2/3.
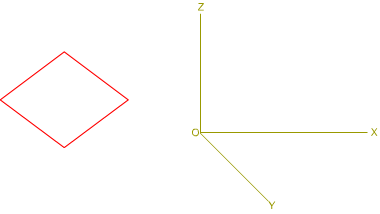 |
En la imagen izquierda tienes un rombo y los ejes
axonométricos X, Y, Z; tienes que dibujar la perspectiva caballera en
cada plano del triedro, de manera que cada diagonal del rombo sea perpendicular
a un eje.
|
Para realizar este ejercicio debes tener en cuenta los siguientes datos:
- Lado del rombo = 75 mm, diagonal mayor = 120 mm, diagonal menor = 90 mm.
- Coeficiente de reducción 2/3.
- Eje XY = 45º.