2.3. Entre circunferencias y rectas
Actividad
Las tangencias entre rectas y circunferencias generalmente se resuelven
aplicando el método de los lugares geométricos: paralelas y
circunferencias concéntricas.
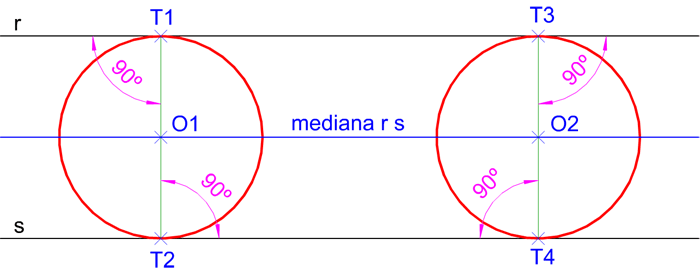
En la imagen superior puedes ver rectas tangentes exteriores a dos circunferencias dadas de igual radio, observa como dichas rectas son paralelas entre sí.
RECTAS TANGENTES A DOS CIRCUNFERENCIAS DADAS:
- Exteriores: se resuelve mediante el método analítico, aplicando el procedimiento de dilatación-contracción, se suman los radios.
- Interiores: se resuelve mediante el método analítico, aplicando el procedimiento de dilatación-contracción, se restan los radios.
- Aplicando homotecia: directa (positiva) e inversa (negativa). Debes aplicar la tercera propiedad de las tangencias entre recta y circunferencia.
| Tangentes Exteriores |
|
|
| Tangentes Interiores |
|
|
CIRCUNFERENCIAS TANGENTES A RECTAS:
- Tangente a dos rectas que se cortan dado el punto de tangencia: se resuelve aplicando la cuarta propiedad de las tangencias entre recta y circunferencia. Método de los lugares geométricos.
- Tangente a tres rectas que se cortan: como las tres rectas conforman un triángulo este problema se resuelve determinando el incentro de dicho polígono, ya que la circunferencia es inscrita. Debes aplicar la cuarta propiedad de las tangencias entre recta y circunferencia. Método de los lugares geométricos.
Caso de estudio
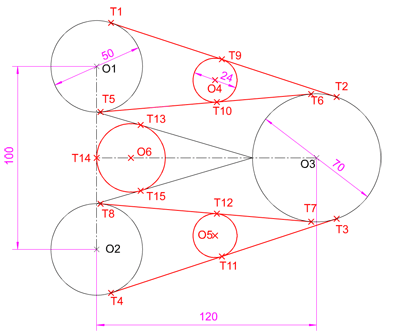Dibuja a escala 1:1 la pieza representada en la imagen izquierda, dimensiones en
milímetros, empleando los conceptos y procedimientos de las tangencias
entre rectas y circunferencias.
¿Necesitas ayuda para resolver este ejercicio?