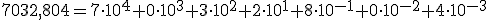2. Sistemas de numeración
Los sistemas digitales actúan mediante la interpretación de señales que toman un número discreto de valores..
Esto hace que sea necesario cuantificar el valor que toman las magnitudes a controlar. Para ello se utilizan diferentes sistemas de numeración, en los que cada uno de los bits tiene un valor u otro según la posición que ocupa dentro del número representado. De manera que la representación de la cantidad expresada por el número N en el sistema de base b, viene representada por la fórmula polinómica:
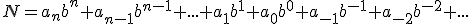
Donde:
- b, es la base del sistema de numeración en que se expresa la cantidad.
- a, son los coeficientes que representan las posibles distintas cifras de la base.
Por ejemplo:
En base octal tendremos: b=8 y 0<ai<8. Todos los números se representan con 8 cifras diferentes que son los comprendidos entre 0-7.
En base decimal tendremos: b=10 y 0<ai<10. Todos los números se representan con 10 cifras diferentes que son los comprendidos entre 0-9.
En base binaria tendremos: b=2 y 0<ai<2. Todos los números se representan con 2 cifras diferentes que son los comprendidos entre 0-1.
Y así sucesivamente.
En nuestro sistema decimal que usamos constantemente, un desglose de un número en forma polinómica sería como ejemplo:
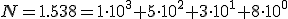
Te puede parecer que la expresión anterior es complicada, sin embargo la utilizas normalmente sin darte cuenta cuando interpretas el significado de una cifra expresada en formato decimal.
Desarrolla la expresión polinómica que se corresponde con la cifra decimal 7.032,804
Los sistemas que utilizan electrónica digital emplean componentes con dos únicos estados posibles (0 y 1). Por ello resulta interesante emplear el sistema de numeración binario (base 2), que utiliza dos dígitos (0 y 1) o también sistemas cuya base sean potencias de dos. Entre estos últimos se utiliza el sistema octal (base ocho), que utiliza ocho dígitos (0, 1, 2, 3, 4, 5, 6 y 7 ), o el hexadecimal (base 16), que utiliza dieciseis dígitos (0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E y F).
Date cuenta de que como este último sistema hexadecimal, precisa dieciseis dígitos diferentes expresados con un solo grafo emplea las primeras letras del alfabeto en mayúsculas una vez que ha utilizado todas las cifras numéricas de un solo dígito.
Por analogía recuerda que nuestro sistema decimal (base 10), utiliza 10 dígitos (0, 1, 2, 3, 4, 5, 6, 7, 8, 9).
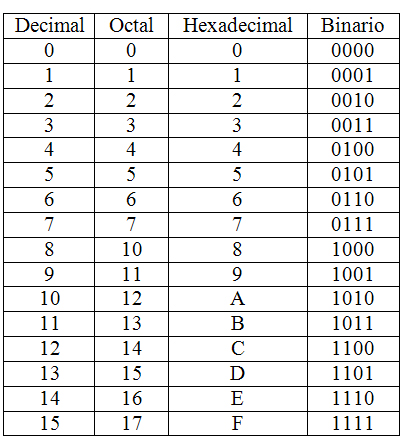
La siguiente tabla muestra la equivalencia entre los primeros dieciseis valores enteros en los cuatro sistemas de numeración más utilizados en los sistemas de control.
 |
|
Imagen 04. Recurso propio.
|
Se llama bit (es la abreviatura de las palabras inglesas Binary digit) a la unidad mínima de información, y solamente puede tomar dos estados posibles el 0, y el 1.
Cuando se expresa una cantidad en cualquier sistema de numeración empleando varios bits, se llama bit más significativo al que ocupa la posición de más a la izquierda, mientras que el bit menos significativo será el que ocupa la posición de más a la derecha.
Se llama byte a un conjunto de ocho bits, el número más alto que se puede representar con un bite es 11111111, que corresponde en decimal al número 255.