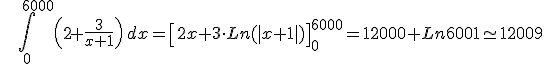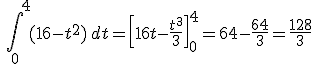1.2. Integración ¿solo es matemáticas y física?
¿Son las integrales algo propio de las matemáticas y la física? Obviamente no, multitud de procesos relacionados con la naturaleza, el medio ambiente, la astronomía o incluso la economía son modelizados gracias a las integrales.
Determinar el reparto de tierras para una herencia o el coste de un motor diésel son situaciones que podemos resolver gracias a las integrales definidas. En este tema vamos a analizar algunas situaciones que son susceptibles de ser resueltas con integrales.
 |
|
Imagen tomada del Banco de Imágenes del ITE. |
Analicemos un problema concreto, el cual, en principio, no guarda relación con la integración, como es determinar el caudal de un río.
Una compaña de electricidad quiere realizar un estudio para construir una central hidroeléctrica. Para ello, realiza estudios en varios ríos, para determinar aquel que mayor caudal tiene y así maximizar los beneficios. Tienen en cuenta que el caudal es la velocidad que lleva el agua de un río, por lo que el caudal en invierno será mayor que en verano y la cantidad de agua durante un periodo de tiempo será el área encerrada entre el eje X y la curva del caudal en el intervalo de tiempo que consideremos.
Una de las opciones que estudia la compañía es construir una presa con
su correspondiente central en el río Andarax. Tras el estudio previo
llegan a la conclusión que el caudal, en miles de hectolitros y en
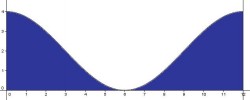
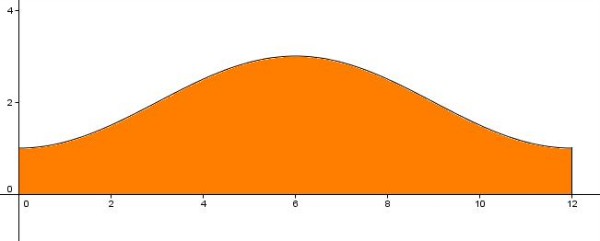
función del mes del año, viene dado por 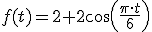 .
.
Analizan la cantidad de hectolitros que pasan durante todo el año por el río y para ello calculan el área encerrada entre el eje X y la función dada.
|
|
Calculan la siguiente integral definida 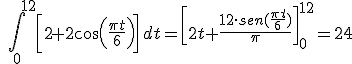 . Por lo tanto pueden afirmar que por el rio Andarax trasncurrirán 24000 hectolitros.
. Por lo tanto pueden afirmar que por el rio Andarax trasncurrirán 24000 hectolitros.
Como indicamos anteriormente, la integración será una herramienta muy útil para muchas ramas de conocimiento, como por ejemplo la economía. Los ingresos o los beneficios de una empresa o los costes de un seguro de coche o del hogar pueden ser estudiados y calculados utilizando técnicas de integración.
Un concepto utilizado en economía es el ingreso marginal, es decir, el ingreso que la compañía percibe al vender una unidad más. Si la función de ingreso es conocido, podemos determinar los ingresos al vender una determinada cantidad si determinamos el área entre la función de ingresos marginales y el eje X.

|
| Fotografía del Banco de Imágenes del ITE. |
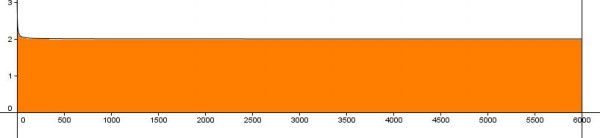
La compañia LumiLumi produce bombillas de alta potencia para la luces de largo alcance de vehículos de gama media. Una empresa dedicada a la fabricación de vehículos le propone la construcción de 6000 bombillas de tipo H4 y tras varios estudios llegan a la conclusión que la función de ingresos para este tipo de bombillas se corresponde con la expresión 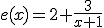 .
.
Por motivos de stock, los directivos tienen que decidir si construir esta nueva bombilla o seguir construyendo la bombilla X7, cuyos ingresos son de 10000 € por la fabricación de 6000 bombillas. Indica cuál bombilla producirá más ingresos para la compañia.

|
| Dibujo del Banco de Imágenes del ITE. |
Algunas compañias, como por ejemplo las dedicadas a la explotación de minas, no se vuelven rentables al transcurrir los años. Aquí los ingresos van disminuyendo, ya que el material extraido disminuye con el paso del tiempo y los costes se van incrementando, ya que se dificulta la extracción de material. La función que nos indica el beneficio en un momento puntual es y = 16 -x2 donde x corresponde a los años transcurridos desde la inauguración y f(x) los beneficios obtenidos en cientos de miles de euros.
Determinar en primer lugar el momento en el que los beneficios se hacen nulos y las ganancias obtenidas desde la inauguración hasta ese momento.
 |
|
Fotografía obtenida del Banco de Imágenes del ITE. |
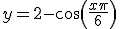 , donde x representa el mes del año y la variable y, las toneladas recogidas.
, donde x representa el mes del año y la variable y, las toneladas recogidas.
|
0
| |
|
6
| |
|
12
| |
|
24
|