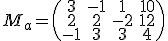1.1. ¡Esto es lo que hay!
 |
| Futbol sala, imagen de malojavio bajo licencia CC by-sa/2.0 |
Se llama ecuación lineal con tres incógnitas a la suma de las tres incógnitas, multiplicadas por números, e igualada la suma a otro número. Por ejemplo, 6·x-2·y+9·z=24.
Esta definición puede ampliarse a cualquier cantidad de incógnitas. La única exigencia es que las variables vayan multiplicadas por números y sumadas. Puede darse que las variables aparezcan en distinto miembro, en ese caso basta agrupar todas las variables en un miembro y en el otro el término independiente. Por ejemplo, la ecuación 6x+9z=24+2y es equivalente a la anterior.
Se llama solución de la ecuación lineal a un conjunto de valores que al sustituirlos en las incógnitas hacen que se verifique la igualdad. Por ejemplo, los valores x=2, y=3, z=2 son solución de la ecuación anterior ya que se verifica que 6·2-2·3+9·2 = 12-6+18 = 24.
Por ejemplo a continuación tenemos un sistema de 3 ecuaciones con tres incógnitas y otro de 2 ecuaciones con cuatro incógnitas.
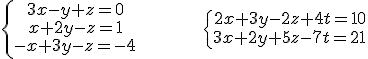
La solución de un sistema de ecuaciones lineales es el conjunto de valores que verifican todas y cada una de las ecuaciones.
Por ejemplo, los valores x=1, y=-3, z=-6 verifican el primer sistema anterior ya que se verifica:
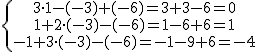
 |
| Fotografía tomada del Banco de Imágenes y sonidos del ITE. |
En un grupo de Bachillerato formado por 35 alumnos los hemos repartido formando tres equipos de baloncesto, dos de balonmano y uno de balonvolea. En otro grupo hemos formado dos de baloncesto, uno de balonmano y dos de balonvolea, juntando en total 29 alumnos. Por último, con 30 alumnos hemos conseguido un equipo de baloncesto, otro de balonmano y tres de balonvolea.
- Si x representa el número de alumnos que forman un equipo de baloncesto, y los del balonmano y z los que componen un equipo de balonvolea, escribe un sistema de tres ecuaciones con esas tres incógnitas que recoja la información anterior.
- Comprueba que x=5, y=7 y z=6 es solución del sistema anterior. ¿Qué representan esos valores?
Una forma muy cómoda de trabajar con un sistema es mediante su forma matricial, pues vamos a poder aplicar todo lo que hemos aprendido hasta el momento en la unidad.
Si tenemos un sistema general 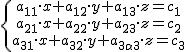 , se agrupan en forma matricial los términos como:
, se agrupan en forma matricial los términos como: 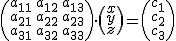 .
.
La matriz 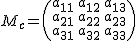 recibe el nombre de matriz de los coeficientes y esta formada, por filas, por los coeficientes de cada una de las ecuaciones y por columnas por los coeficientes de cada variable.
recibe el nombre de matriz de los coeficientes y esta formada, por filas, por los coeficientes de cada una de las ecuaciones y por columnas por los coeficientes de cada variable.
La matriz 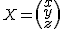 es la matriz de las incógnitas y
es la matriz de las incógnitas y 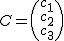 la matriz de los términos independientes.
la matriz de los términos independientes.
Se llama matriz ampliada a la que se obtiene añadiéndole a la matriz de los coeficientes la columna de los términos independientes. 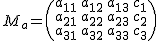 .
.
Dado el sistema 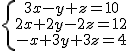 escríbelo en forma matricial y comprueba que, aplicando las operaciones con matrices, esa expresión es equivalente al sistema original.
escríbelo en forma matricial y comprueba que, aplicando las operaciones con matrices, esa expresión es equivalente al sistema original.
¿Cuál sería la matriz ampliada en ese sistema?
Dos sistemas de ecuaciones lineales son equivalentes cuando tienen exactamente las mismas soluciones, es decir, todas las soluciones del primer sistema lo son del segundo y viceversa.
Las propiedades que permiten convertir un sistema de ecuaciones en otro equivalente ya las has visto en cursos anteriores y son muy parecidas a las que hemos utilizado para aplicar Gauss en los temas anteriores. Si no las recuerdas o quieres repasarlas puedes hacerlo en el siguiente enlace.

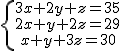 .
.
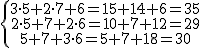
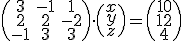 y si en ella multiplicamos las matrices del primer miembro, obtendríamos entonces una igualdad entre matrices que sería
y si en ella multiplicamos las matrices del primer miembro, obtendríamos entonces una igualdad entre matrices que sería 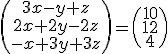 y si igualamos miembro a miembro se obtiene el sistema inicial.
y si igualamos miembro a miembro se obtiene el sistema inicial.