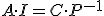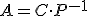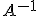2.5. Aprovechando la matriz mareada
|
|
Ahora ya conoces la forma de marear algunas matrices, ya que hay otras que no se dejan por mucho que lo intentes. Te hemos mostrado dos métodos para marearlas, pero recuerda que debes marearlas a ellas sin marearte tú y, para ello, debes tener claro los conceptos que estás utilizando, cuándo puedes utilizarlos y cómo debes utilizarlos. Para aclararte un poco todo esto nos encontramos ahora aquí.
 |
| Planta del cacao. Imagen obtenida del banco de imágenes del ITE. |
 |
| Regiones productoras de cacao. Imagen obtenida del banco de imágenes del ITE |
Una empresa de cacao importa este alimento desde dos zonas situadas cerca de la frontera de Colombia llamadas Cimborazo y Cotopaxi. Durante los tres primeros meses del año, por cada saco que exportaba de la primera zona pensaban pagar 2 euros y por cada saco de la segunda pagaba 3 euros.
Pero ahora llega una época de crisis y han decidido pagar 1 euro por cada saco venga de la zona que venga. El administrador de la empresa ha estado echando cuentas y ha obtenido una tabla en la que recoge el dinero que deberían haber pagado si hubieran mantenido el precio incial y el dinero que realmente van a pagar cada uno de los meses:
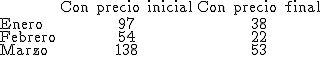
Un segundo administrador se pregunta ¿Cuánto deberían haber pagado cada mes si hubiesen pagado 1 euro por cada saco proveniente de Cimborazo y 2 por cada saco proveniente de Cotopaxi. Evidentemente, para calcular esto, deberá conocer primeramente el número de sacos que ha comprado la empresa en cada una de las zonas. A ver si puedes echarle una mano.
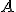 solución del ejercicio anterior y escribe debajo la matriz de lo que hubieran pagado cada mes según los cálculos del segundo administrador
solución del ejercicio anterior y escribe debajo la matriz de lo que hubieran pagado cada mes según los cálculos del segundo administrador
1.- La matriz 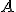 es:
es:
2.- Lo que hubieran pagado cada mes según los precios del segundo administrador sería
Enero:
Febrero:
Marzo:
Ahora te proponemos un ejercicio más directo en el que observes que podemos resolver ecuaciones con matrices. En este caso la ecuación matricial que te proponemos es la siguiente:
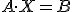
Donde las matrices que aparecen son: 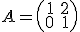 y
y 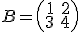 .
.
En este caso, la matriz 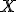 es
es



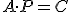
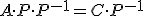 por tanto, como el producto de una matriz por su inversa es la matriz identidad
por tanto, como el producto de una matriz por su inversa es la matriz identidad