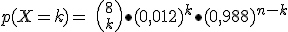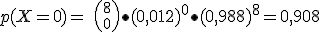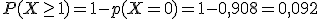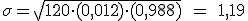2.3.- ¿Será por parámetros?
 |
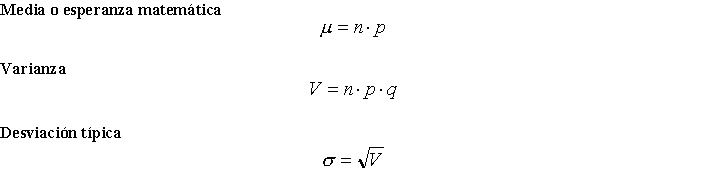En el apartado 1.2, ya se ha comentado que cada variable aleatoria de caracteriza por sus parámetros. La B(n, p) no va ha ser distinta a las demás.
¿Recuerdas la tabla de la variable aleatoria que designaba el número de vehículos destinados a taxis?
| X | 0 |
1 |
2 |
3 |
| pi | 0,729 | 0,243 | 0,027 | 0,001 |
Recordando las fórmulas de la esperanza, varianza y la desviación típica, tendremos:
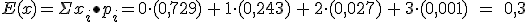
Observa que E(x)= 3·(0,1) = n·p
De la misma forma para la varianza:
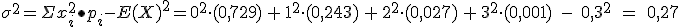
También, la varianza depende de n y p, es decir ,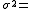 
n·p·(1-p)=3·(0,1)·(0,9) = 0,27.
El resultado de estas conclusiones lo vamos a ver en el siguiente cuadro resumen de la Binomial.
Resumen de la Binomial
Ejemplo o ejercicio resuelto
|
|
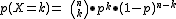
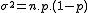
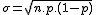
9. Avión comercial:Imagen de soyesoterica.com bajo licencia de Creative Commons |
La probabilidad de que un avión llegue con retraso a un determinado aeropuerto es de 0,012. En una hora llegan al aeropuerto 8 aviones. ¿Cuál es la probabilidad que ninguno llegue con retraso? ¿Cuál es la probabilidad de que alguno llegue con retraso?
Si en un día se esperan la llegada de 120 aviones ¿qué media de aviones llegarán con retraso? ¿Cuál sería en este caso la desviación típica?
AV - Pregunta de Elección Múltiple|
a) Ninguna por que es muy raro ese grupo
| |
|
b)1.320.000
| |
|
c) 1.320
|
|
a) 0,60
| |
|
b) 0
| |
|
c) 0,3
|
|
a) 0,0051
| |
|
b) 0,051
| |
|
c) 0,51
|
