1.1.- La forma de distribuir es diversa.
 |
En el gráfico de arriba se ha representado los datos del juego de los chinos como aparece en la tabla del apartado anterior (que abajo la reproducimos de nuevo). En el eje de abscisas (X) las posibles sumas entre los dos jugadores y en el de ordenadas (Y) la frecuencia relativa o probabilidad.
| X | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| frecuencia absoluta |
1 | 2 | 3 | 4 | 3 | 2 | 1 |
| p(x) | 1/16 | 2/16 | 3/16 | 4/16 | 3/16 | 2/16 | 1/16 |
Una variable aleatoria es una función que asocia a cada elemento del espacio muestral un número real.
Cada variable aleatoria lleva asociada una función de probabilidad, que hace corresponder a cada valor de la variable (x) la probabilidad de que ocurra. Se denota por:
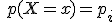
Nota: En el ejemplo anterior la probabilidad de que la suma de monedas sea 4 es: p(X=4)= 4/16
 |
|
2. Autobús: Imagen de ceiplosalados bajo licencia de Creative Commons |
El autobús escolar de Pablo, suele pasar a recogerlo entre las 8:35 y las 8:40 el tiempo que espera es una icógnita para él, en los últimos 5 días tomó estos datos en segundos desde que llega a la parada hasta que aparece el bus.
| X=tiempo en segundos de espera | 0 a 30 | 30 a 60 | 60 a 120 | 120 a 240 | mas de 240 |
| frecuencia absoluta | 1 | 1 | 1 | 1 | 1 |
| Probabilidad | 0.2 | 0.2 | 0.2 | 0.2 | 0.2 |
A diferencia del juego de los chinos la variable aleatoria toma valores dentro de un intervalo y es de probabilidad nula el que se den dos resultados puntuales iguales.
Puedes comprobarlo tú mismo la probabilidad que el autobús llegue a los 20 segundos y 19 centésimas dos veces es cero.
A diferencia con las variables que sí pueden tomar valores concretos más de una vez (variables discretas) están las que no (variables continuas)
Las variables aleatorias pueden ser de dos tipos:
Variables discretas: Son aquellas que, aunque también puedan tomar valores infinitos, entre un valor y el siguiente no es necesario pasar por los puntos intermedios.
Ejemplo: El número de monedas en una mano de los chinos puede ser 2 y en otra 3, sin embargo, nunca tomará ningún valor entre 2 y 3.
Variables continuas: Son aquellas que necesariamente para pasar de un valor a otro pueden tomar los infinitos valores intermedios.
Ejemplo: Si el autobús aparece a los 30 segundos un día y a los 32 otro puede venir en cualquier día entre los 30 y 32.
Verdadero Falso
Verdadero Falso
Verdadero Falso