3. La aspirina Bayes
 |
| aspirina de action datsun, CC by-nc-sa 2.0 |
Muchas veces, ante un malestar físico habrás escuchado: tómate una aspirina y se te pasará.
La aspirina parece la solución común a cualquier molestia. Igual ocurre en la probabilidad condicionada, que la solución a muchos de sus problemas la proporciona el Teorema de la Probabilidad Total y el Teorema de Bayes.
Veamos ejemplos de problemas resueltos por los dos teoremas mencionados.
Teorema de la Probabilidad Total
Sea A1, A2, ...,An un sistema completo de sucesos tales que P(Ai)≠0, y sea B un suceso cualquier del que se conocen las probabilidades condicionadas P(B/Ai), entonces la probabilidad del suceso B viene dada por la expresión:
P(B)=P(A1)·P(B/A1) + P(A2)·P(B/A2) + ...+ P(An)·P(B/An)
| |
¿Tienes aún ganas de yogur? Mejor que sea así, porque para aclarar la expresión anterior vamos a echar mano otra vez de ellos.
¿Cuál es la probabilidad de que Lola cogiera un yogur de plátano? ¿Desnatado o normal? Da igual, la cuestión es que sea de plátano. Pues ese es el suceso que en el Importante de arriba llama B = "yogur de plátano".
¿Y los Ai, quiénes son? Pues en nuestro caso sólo hay dos Ai. A1="yogur desnatado" y A2="yogur no desnatado". Lo de completo quiere decir que ellos llenan todo el espacio de sucesos, es decir, un yogur o es desnatado o no desnatado, no queda otra.
Ha llegado el momento de explicar la fórmula:
P(B) = P(A1)·P(B/A1) + P(A2)·P(B/A2),
no quiere decir otra cosa que la probabilidad de que el yogur sea de plátano es igual a la probabilidad de que sea desnatado, por la probabilidad de que sea de plátano siendo desnatado, más la probabilidad de que no sea desnatado, por la probabilidad de que sea de plátano no siendo desnatado.
¡Uf! Algo largo, pero se entiende. Verás, para llegar a desnatado por el árbol se pude coger por la rama desnatado o por la rama de no desnatado. El primer producto es la primera rama, y el segundo producto es la segunda rama. La suma de ambas nos da la probabilidad de que cogiera un yogur de plátano.
Queda entonces: P("yogur de plátano") = 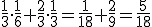 .
.
Lo que es cierto, pues de 18 yogures, sólo 5 son de sabor a plátano.
Debemos actuar de forma parecida a la explicada anteriormente. Completa los espacios en blanco.
Llamamos B="yogur de ", A1="yogur " y A2="yogur desanatado".
Entonces, aplicando el Teorema de la Probabilidad Total, tenemos que: P(B) = P(A1)·P( /A1) + P(A2)·P(B/A2).
Sustituimos: P("yogur de fresa") = 1/ · 1/3 + /3 · 1/ = 1/9 + 1/9 = 2/9.
Demos una vuelta de tuerca más a lo yogures (al final los convertiremos en batidos).
Tomas un yogur al azar, sin mirar, ni el paquete ni el sabor. Resulta que es de plátano, ¿cuál es la probabilidad que el "pack" elegido sea el desnatado?
Observa, sabemos el suceso final ("yogur de plátano"), y nos preguntan por un suceso intermedio ("yogur desnatado"). Es decir, nos pregunta:
P("yogur desnatado" / "yogur plátano")
Teorema de Bayes
Sea A1, A2, ...,An un sistema completo de sucesos tales que P(Ai)≠0, y sea B un suceso cualquiera, con P(B)≠0, entonces:
![]() para j= 0,...,n
para j= 0,...,n
Para practicar más los teoremas de Bayes y probabilidad total puedes entrar en el siguiente enlace de Ed@d del MEC.
 |
| nuevos médicos de Fotos Gov/Ba con licencia cc by 2.0 |
Según una encuesta del Servicio de Salud, uno de cada cuatro médicos de cabecera receta a sus pacientes el 80% de las veces aspirina, el 8% antibiótico y el 12% ibuprofeno. En tanto que, tres de cada cuatro recetan el 50% de las veces aspirina, el 20% antibótico y el 30% ibuprofeno.
A los sanitarios del primer tipo les llamaremos "Médico 1", y a los del segundo "Médico 2"
Elegimos un paciente al azar. ¿Nos preguntamos por el valor de las siguientes probabilidades?
a) De que habiendo sido atendido por un médico del primer tipo, le receten ibuprofeno.b) De que le receten ibuprofeno
c) De que habiendole recetado ibuprofeno, lo haya atendido un médico del primer tipo.
Completa los espacios en blanco.
a) ("Le recetan ibuprofeno" /"Médico 1") = 0,
b) Aplicamos el Teorema de la Probabilidad :
P("ibuprofeno") = P("Médico 1") · P(" "/"Médico 1") + P(" Médico ") · P("ibuprofeno"/"Médico 2") =
0, · 0,12 + 0,75 · 0, = 0,26
c) Ahora aplicamos el Teorema de :
P("Médico 1" / "ibuprofeno") = P("Médico 1" y "ibuprofeno") / P("ibuprofeno") = (0,25 · 0,
) / 0,26 = 0,12
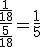 .
.