2. ¡Qué mal repartido está el mundo!
Al igual que pasa en el mundo, las variables estadísticas no siempre están bien repartidas, de tal forma que la media puede no ser representativa si hay valores dispares que le afecten. Para eso tenemos las medidas de dispersión, que nos informan de la concentración de esos datos dentro de la variable.

|
| Partido España-Israel de Berts @idar, CC by-nc-sa 2.0 |
 |
|
Japón economía de artemuestra con licencia cc by-sa/2.0 |
Imaginemos que estamos interesados en comprar en bolsa acciones de una determinada empresa. Para saber si es una inversión segura, investigamos la evolución del precio de las acciones en el último año. Por supuesto, hemos calculado previamente cuál ha sido el precio medio de las acciones y mirando el resto de los valores podremos decir que si muchos días el precio ha estado alejado de la media (por debajo o por encima), diremos que la inversión es arriesgada o volátil. Y por el contrario, si la mayoría de los días el precio ha estado cerca de la media diremos que la inversión es segura.
La medida estadística que nos indica esta variación de los datos respecto de la media es la varianza.
La varianza mide la dispersión de una muestra en función de la diferencia (la distancia) de cada uno de los elementos de la muestra con el valor medio de la misma. Se representa por s2.
Se calcula mediante la fórmula:
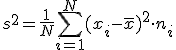
La desviación típica es la raíz cuadrada positiva de la varianza. Se representa por σ=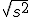 .
.
Aunque tanto la varianza como la desviación típica son medidas de la variación con respecto a la media y tienen un significado semejante, la desviación típica se utiliza con más frecuencia porque se expresa en las mismas unidades que los valores de las variables. Al contrario que la varianza, cuyos valores se expresan en unidades al cuadrado.
No debes asustarte al ver la fórmula que es necesario utilizar para calcular la varianza, y por tanto la desviación típica.
Recuerda que N no es más que la suma de las frecuencias absolutas, es decir 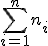 , y
, y 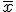 es la media.
es la media.
Además, realizando ciertos cálculos, es posible obtener una fórmula más operativa que la anterior:
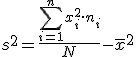
Veamos con un ejemplo cómo se aplica la expresión anterior.
Volvemos a la encuesta del INE sobre actividades de formación en el año 2007 de las personas adultas en España. Veamos en la siguiente presentación los pasos que hay que dar para calcular la varianza y la desviación típica de los datos obtenidos en dicha encuesta.
|
|

|
|
1st march de obo-bobolina con licencia cc by-nc/2.0 |
Para defenderse de la varianza lo más común es mejorar la gestión de los recursos propios (banca), para que "un zarpazo de la varianza" no termine en "bancarrota". Es decir que una racha negativa no acabe con toda nuestra banca y podamos seguir jugando hasta que llegue una racha positiva.
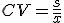
Supongamos las dos empresas anteriores con los siguientes datos:
| Empresa 1 |
Empresa 2 |
|
| Desviación típica |
10€ | 10€ |
|
Media (precio medio por acción) |
50€ | 20€ |
¿En cuál de las dos empresas debemos invertir?
En el apartado anterior veíamos como el INE desglozaba la encuesta sobre actividades de formación, en enseñanzas formales y no formales. Los datos eran los siguientes:
| Tramos de edad |
Personas que cursaron enseñanza formal |
Personas que cursaron enseñanza no formal |
| [25, 35) |
896270 | 2475505 |
| [35, 45) | 334895 | 2224578 |
| [45, 55) | 200511 | 1496676 |
| [55, 65) | 85918 | 742246 |
| [65, 75) |
26912 | 277585 |
Halla la desviación típica y el coeficiente de variación para cada una de las modalidades de enseñanza. Compara los resultados que hayas obtenido.