2. Soy muy aplicada
En la primera parte del tema, hemos tratado la representación de funciones y la interpretación de sus gráficas. En ella, hemos hecho uso de la derivada a la hora de estudiar la monotonía y la curvatura. Pero éstas, son sólo algunas de las aplicaciones de las derivadas, puesto que hay muchas más.
Las derivadas se aplican también en la resolución de problemas de otras áreas y ramas de conocimiento tan dispares como las Física, la Economía, la Medicina, en Tecnología Industrial, en muchos campos de la Ingeniería ...
Pero, espera un momento porque nunca viene mal un poco de reflexión y de pausa matemática en clave de humor. Es por ello, por lo que proponemos que veas estas dos versiones del curiosísimo
"Romance de la Derivada n-ésima y el ArcoTangente"
¿Qué te han parecido los vídeos? Simpáticos, verdad. ¡Qué imaginación tienen alguno/as y qué bien interpretan otro/as!
Tras este pequeño paréntesis, continuamos con el tema. Veremos a continuación un par de ejemplos de aplicación de las derivadas.
El primero es un problema de aplicación al campo de la Medicina (efectos de medicamento en pacientes).
Comenzamos ...
Ejemplo o ejercicio resuelto
|
|
|
La función que mide la concentración de un determinado medicamento en el cuerpo de un paciente trascurridas t horas desde que se lo toma, viene dada por la siguiente expresión:
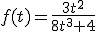
(a) ¿En qué intervalos horarios aumenta y disminuye dicha concentración?
(b) ¿A qué hora es máxima la concentración del medicamento en el cuerpo del paciente?
.jpg)
AV - Actividad de Espacios en Blanco
|
|
|
Si
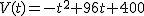
es la función que nos indica el número de ejemplares que se venden de un determinado libro en función de los días, t, transcurridos desde que dicho libro se puso en el mercado.
(a) ¿Cuántos ejemplares se vendieron el mismo día que el libro se puso a la venta?
Se vendieron ejemplares.
(b) El intervalo de días en que las ventas aumentan.
Las ventas aumentan en el intervalo [ , )
Crecen los primeros días.
(c) La función V(t) alcanza un máximo relativo, que indica el día que mayor número de ejemplares se vende. ¿Para qué valor de t se obtiene dicho máximo? ¿Cuántos libros se vendieron ese día?
El día t = se vendieron libros.
(d) ¿Cuántos días pasan hasta que no se vende ningún libro?
A los días no se vende ningún ejemplar del libro.
Nota: Consideraremos que t=0 indica el día que el libro se pone a la venta.
.jpg)
.jpg)
.jpg)
.jpg)
Para terminar con algunas de las aplicaciones de la derivada ya que podríamos seguir dando ejemplos durante un largo tiempo, os dejamos sendos vídeos de su aplicación a la Física que, concretamente, ilustran los siguientes conceptos:
· Velocidad como derivada de la distancia y,
· Aceleración como derivada de la velocidad.
Objetivos
En los siguientes enlaces al Proyecto Descartes, puedes practicar más y ampliar tus conocimientos con distintos problemas de aplicaciones de la derivada que podrás resolver con ayuda de escenas interactivas de Descartes.