1. De monótono, nada.
El crecimiento y el decrecimiento de una función es algo que ya hemos estudiado antes ¿lo recuerdas? Básicamente una función es creciente si, al aumentar la variable independiente, x, también aumenta el valor de la función, f(x). Es decreciente, si al aumentar el valor de x, disminuye el de f(x). No olvides que las gráficas se "leen" de izquierda a derecha.
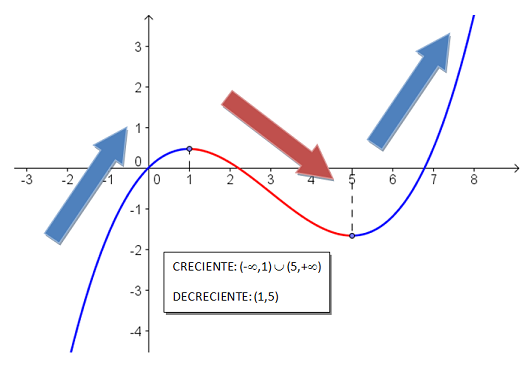
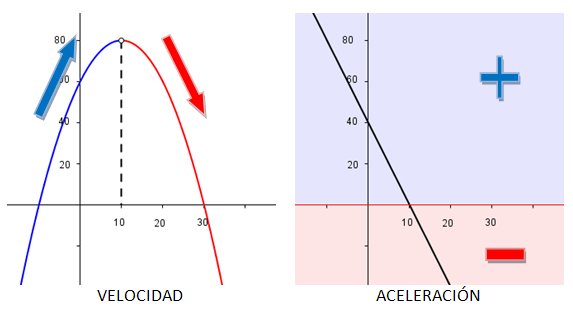
Cuando hablamos de monotonía, nos estamos refiriendo al comportamiento de una función respecto a su crecimiento o decrecimiento.
Sea f una función derivable en un intervalo (a, b), entonces es:
- Creciente en el intervalo (a,b) si
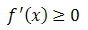 en todo el intervalo (a,b)
en todo el intervalo (a,b) - Decreciente en el intervalo (a,b) si
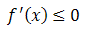 en todo el intervalo (a,b)
en todo el intervalo (a,b)
En la siguiente escena de geogebra tienes dos ejemplos, una función polinómica y una racional, en la que puedes comprobar que se cumple lo que acabamos de ver:
| Función f(x) |
Derivada f ' (x) |
| Creciente | Positiva (con linea discontinua) |
| Decreciente |
Negativa (con linea discontinua) |
Como ya hemos comentado, lo relevante del importante anterior, es que ya no es necesario dibujar la gráfica para estudiar la monotonía. A continuación tienes un ejercicio resuelto para que veas cómo hacerlo. Después hay uno que tendrás que resolver tú.
En una empresa están teniendo pérdidas económicas, por lo que deciden poner en marcha una serie de medidas a lo largo de los próximos 6 meses con las que pretenden remontar y obtener beneficios al finalizar dicho periodo.
Según sus cuentas, los beneficios obtenidos por la empresa al poner en marcha el plan vienen dados por la función ![]() , donde x es el número de meses.
, donde x es el número de meses.
Vamos a comprobar si con este plan de medidas la empresa mejorará los beneficios. Para ello tendrás que estudiar los intervalos de crecimiento y decrecimiento de los beneficios de la empresa.
- Función derivada:
Para comenzar, calcula la derivada de la función f(x) y completa los espacios en blanco (incluye los signos correspondientes):
f ' (x) = x x x
- Obtener las raíces de la derivada:
Resuelve la ecuación f ' (x) = 0 para obtener las raíces. Como es un polinomio de grado mayor que dos, tendrás que resolver con la Regla de Ruffini.
Las soluciones son (de menor a mayor) x= , x= , x= .
- Estudiar el signo de la derivada:
Hemos obtenido cuatro intervalos. Estudia el signo de la función derivada en cada intervalo:
En el intervalo (-∞, ) la derivada es (positiva/negativa) .
En el intervalo ( , ) la derivada es (positiva/negativa) .
En el intervalo ( , ) la derivada es (positiva/negativa) .
En el intervalo ( ,+∞) la derivada es (positiva/negativa) .
- Estudiar la monotonía:
Teniendo en cuenta los resultados del apartado anterior, podemos decir que en (-∞, )U( , ) la función es (creciente/decreciente) , y que en ( , )U( ,+∞) la función es .
- Solución del problema: