1. Separadas hasta el infinito
"Sinuhé llegó a la ciudad de Luxor, y al acercarse a un pozo en el que beber agua, se encontró con Pazair, un egipcio que había conocido días atrás.
- Saludos Pazair, me alegro de encontrarte de nuevo, ¿cómo es que no hemos coincidido por el camino? - preguntó Sinuhé.
- Quisieran los dioses que volviéramos a encontrarnos, debemos haber seguido caminos paralelos desde que nos despedimos.
- Lo dudo amigo Pazair, pues los caminos paralelos nunca han de encontrarse."
Si trabajas con rectas en el plano puedes observar que sólo pueden situarse de tres formas: o no se cortan (paralelas), o se cortan en un punto (secantes), o una está sobre la otra (coincidentes).
¿Qué condiciones deben darse en cada caso? O dicho de otra forma: si sólo tenemos las ecuaciones de ambas rectas sin su representación gráfica, ¿cómo podemos saber cuál es la posición relativa de ambas?
En el siguiente applet de Geogebra puedes experimentar cómo cambia la posición relativa de dos rectas al modificar uno de los puntos por los que pasa (A o P) y sus pendientes (ms y mr).
Utilízalo para contestar las preguntas que se hacen a continuación, teniendo en cuenta
que las ecuaciones de las rectas vienen dadas en la forma r = Ax+By=C, s = A'x+B'y=C'.
Sus vectores directores u y v son proporcionales
| |
Sus vectores directores u y v no son proporcionales
| |
Sus pendientes son diferentes
| |
Sus pendientes son iguales
| |
A / A' = B / B'
| |
Sus vectores directores u y v son proporcionales
| |
Sus vectores directores u y v no son perpendiculares
| |
Sus pendientes son iguales
| |
A / A' = B / B' ≠ C / C'
| |
Tienen, como mínimo, tres puntos en común
| |
Sus vectores son proporcionales y tienen un punto en común
| |
A / A' ≠ B / B'
| |
Aquí tienes un resumen de lo anterior para que puedas resolver las actividades:
Completa los espacios en blanco de las siguientes actividades:
a) Las rectas 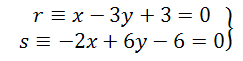 son (secantes/paralelas/coincidentes):
son (secantes/paralelas/coincidentes):
b) De las siguientes rectas, ¿cuáles son secantes con la número 1? La y la
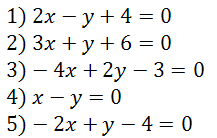
c) Si una recta pasa por los puntos A=(1,0) y B=(3,1), y otra por los puntos P=(-2,4) y Q=(0,3), ambas rectas son (secantes, paralelas, coincidentes)
d) Averigua el valor de m para que ambas rectas sean paralelas: m =
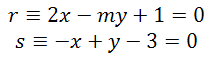
"Sinuhé y Pazair se reunieron al día siguiente en la salida de la ciudad para proseguir su camino.
- De nuevo nos separamos, amigo Sinuhé, pues nuestros rectos caminos se alejan.
- Desde luego, unos 50º de separación, me atrevo a aventurar.
- ¿Acaso puedes saberlo con sólo mirar?
- Podría calcularlo fácilmente, y apenas retrasaría nuestra marcha."
Calcular el ángulo que forman dos rectas secantes es sencillo. De hecho ya debes saber hacerlo, pues es el mismo que forman sus dos vectores directores. También puede calcularse a partir de las pendientes de ambas rectas. Dependiendo de los datos que tengas, deberás usar una u otra fórmula:
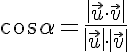
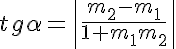
No es necesario que calculemos las ecuaciones de las rectas, pues nos basta con calcular sus vectores directores con los siguientes datos:
A = Luxor = (23.70, 32.60)
B = Al Baghdadi = (26.64, 32.61)
C = Al Bayadiyah = (25.67, 32.66)
Calcularemos los vectores u=AB y v=AC:
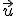 = (1.94, 0.01)
= (1.94, 0.01)
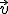 = (1.97, 0.06)
= (1.97, 0.06)