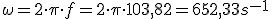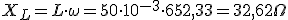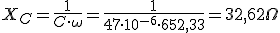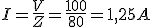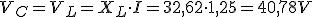7. Circuitos osciladores
 |
|
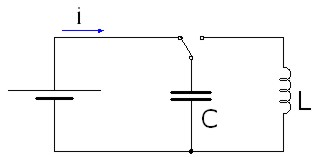
Imagen 45: Circuito oscilante LC. |
Como puedes deducir, en la posición que indica la figura superior, la corriente pasará por el condensador hasta que se complete su carga. Llegado este punto actuamos sobre el conmutador cambiando su posición (imagen inferior), por lo que el condensador se descargará sobre la bobina. A medida que comienza la descarga sobre la bobina en esta se producirá una tensión por efecto de la autoinducción, opuesta a la causa que la origina y a medida que ésta va aumentando la corriente que la recorre irá disminuyendo.
 |
|
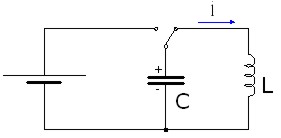
Imagen 46: Circuito oscilante LC.
Fuente: Elaboración propia. |
Llegará un momento en que al descargarse el condensador comenzará la descarga de la bobina sobre aquel, pues el conmutador sigue en la posición que lo habíamos dejado.
 |
|
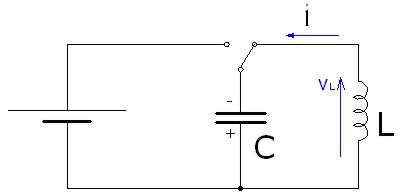
Imagen 47: Circuito oscilante LC. |
Una vez finalizada la carga del condensador, la tensión en la bobina habrá desaparecido, momento en que comenzará un nuevo ciclo de descarga del condensador sobre la bobina.
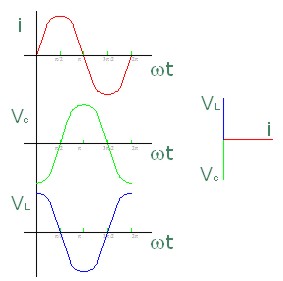
Si tratamos de representar como han ido cambiando los valores de la corriente por el circuito y cómo han evolucionado las tensiones en condensador y bobina observaremos que:
 |
|
Imagen 48: Representación senoidal de i, Vc y Vl en un circuito oscilante LC. |
 |
|
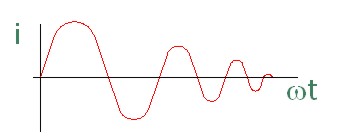
Imagen 49: Amortiguación de la onda senoidal en un circuito oscilante LC. |
Decimos que un circuito es resonante cuando la corriente que circula por él es máxima. Eso sucederá cuando R = 0 y por lo tanto XL = XC con lo cual una anula a la otra. De aquí deducíamos:
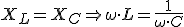 |
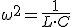 |
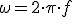 |
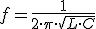 |
Vemos pues como la frecuencia de resonancia depende directamente de la inducción de la bobina en Henrios y de la capacidad del condensador en Faradios, para obtener Hertz.
|
Video 2: Puente sobre el río Tacoma Fuente: Youtube |