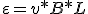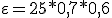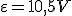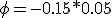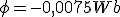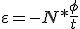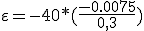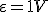2.2. Ley de Faraday
Como recordaras la fuerza electromotriz viene dada por:
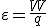
|
Asi pues
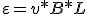
|
Al desplazarse el conductor, durante un tiempo, el flujo va a disminuir, vamos a suponer que es un diferencial de tiempo "dt" y también el area del conductor disminuirá, siendo este area un diferencial de superficie "ds"
Por lo tanto, y teniendo en cuenta que
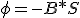
|
y sabiendo que dф = diferencial de flujo magnético, podemos realizar el siguiente desarrollo matemático.
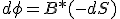
|
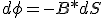
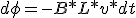
|
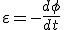
En el caso de tener "N" espiras llegamos a
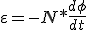
Por lo tanto la Ley de Faraday nos dice que el valor de la fuerza electromotriz inducida no depende de las causas que provocan la variación del flujo, solo de la mayor o menor rapidez con que varia el flujo a través de la superficie limitada por el número de espiras que posee.