1.2. Circunferencias
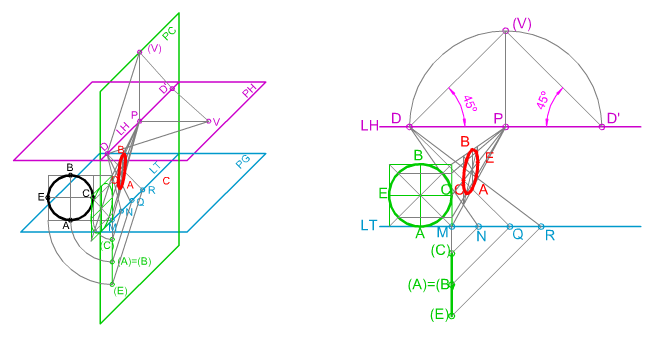
La posición de la circunferencia normalmente será ortogonal respecto del Plano Geometral, pudiendo ser perpendicular u oblicua al Plano del Cuadro.
En la imagen superior puedes ver cómo se ha determinado la perspectiva frontal de una circunferencia perpendicular a ambos planos.
Circunferencia perpendicular al Plano del Cuadro y al Plano Geometral.
Este primer caso analizaremos cómo se obtiene perspectiva cónica frontal de una circunferencia perpendicular al Plano Geometral y al del Plano del Cuadro.
En la animación inferior puedes, ver de manera detallada, cómo hemos determinado dicha perspectiva.
Circunferencia perpendicular al Plano del Cuadro y oblicua Geometral.
La perspectiva cónica oblicua de una circunferencia perpendicular al Plano Geometral y oblicua al del Plano del Cuadro no debe representar dificultad alguna; ya que solamente es necesario representar la proyección cónica del cuadro que lo inscribe, según el método de los puntos.
En la animación inferior te mostramos el procedimiento a seguir.
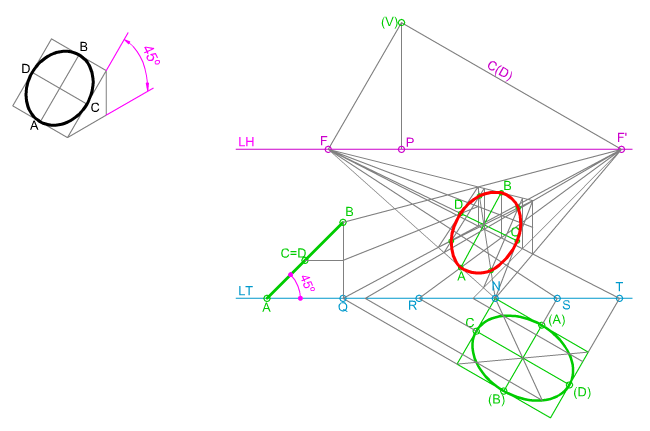 |
| En la imagen superior puedes ver cómo se ha trazado la proyección cónica Oblicua de una circunferencia contenida en un plano que forma 45º con el Plano Geometral (PG) y oblicuo al Plano del Cuadro (PC), dado su abatimiento sobre dicho plano.
Para su dibujo conocemos la posición de la LT y la LH así como el abatimiento sobre el PC del punto de vista (V). Te pedimos que apliques los contenidos y procedimientos adquiridos hasta ahora para su resolución mediante las herramientas de dibujo tradicionales. |