3.1. Pirámides
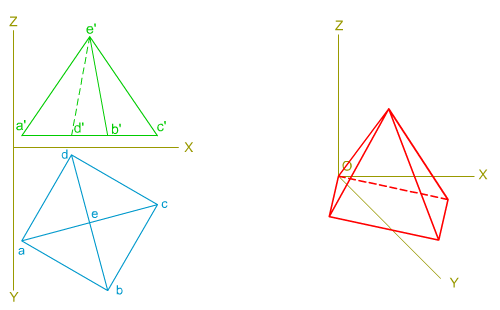
Como vimos en el tema anterior, el trazado de su perspectiva es similar al del Tetraedro, salvo por la determinación de su altura que siempre nos vendrá dada.
Dado que la base de estas superficies debe ser un polígono regular (triángulo equilátero, cuadrado, pentágono, hexágono, etc..) la resolución de cualquier perspectiva caballera debe pasar primero por la de dicha figura plana.
Así pues, siempre comenzaremos dibujando la perspectiva de la planta y luego determinaremos el vértice de la altura.
En la imagen superior te mostramos la perspectiva de una pirámide regular de base cuadrangular, según sus vistas diédricas dadas.
Aristas bases oblicuas a los ejes axonométricos (base triangular).
Como la pirámide es regular la base debe ser un triángulo equilátero, por lo que tendrá cierta similitud con el trazado del Tetraedro.En este caso particular uno de los vértices está contenido el centro O del triedro.
En la animación inferior te mostramos el procedimiento a seguir para trazar la perspectiva caballera de dicha pirámide.
Aristas bases oblicuas a los ejes axonométricos (base cuadrangular).
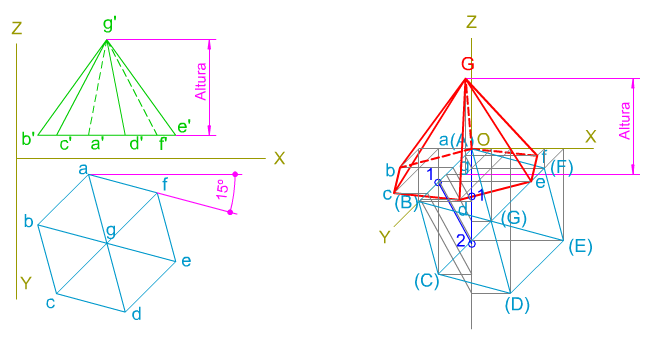
En este caso particular hemos dispuesto una de las aristas base con un ángulo de 30º grados respecto del eje de coordenadas axonométrico X.En la animación inferior te mostramos cómo se determina, mediante abatimiento de la planta sobre el plano XOZ, la perspectiva de dicho poliedro.
|
|
| En la imagen superior te mostramos cómo se ha trazado la perspectiva caballera de una pirámide regular ABCDEFG de base hexagonal apoyada en el triedro XOY por su base ABCDEF.
Conocemos sus proyecciones diédricas, siendo sus aristas bases oblicuas a los ejes axonométricos. Te pedimos que apliques los contenidos y procedimientos adquiridos hasta ahora para su resolución mediante las herramientas de dibujo tradicionales. |