2.1. Tetraedro
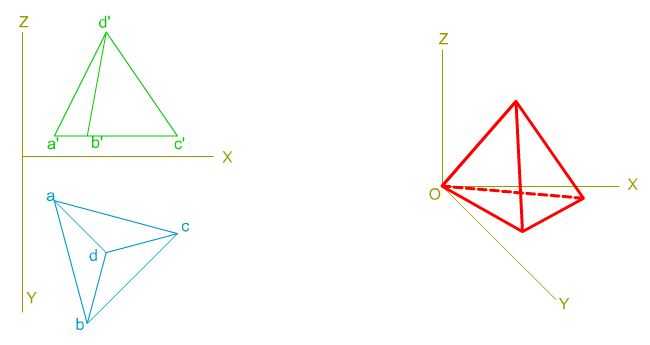
Podemos aplicar lo aprendido en su representación para obtener la perspectiva caballera de las pirámides regulares.
En la imagen superior puedes ver cómo se ha determinado la perspectiva caballera de un tetraedro cuyas aristas básicas son oblicuas a los ejes de coordenadas axonométricos.
Arista base paralela a un eje axonométrico.
En este caso una de las aristas base está contenida en uno de los ejes de coordenadas axonométrico.
En la siguiente animación puedes ver cómo se ha trazado la perspectiva caballera de dicho poliedro según un coeficiente de reducción dado.
Aristas bases oblicuas a los ejes axonométricos.
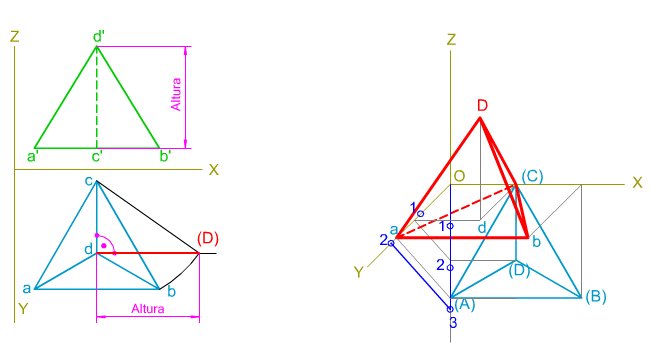
En este caso particular hemos dispuesto una de las aristas base con un ángulo de 15º grados respecto del eje de coordenadas axonométrico X.
En la animación inferior te mostramos cómo se determina la perspectiva de dicho poliedro.
|
|
| En la imagen superior puedes ver cómo se ha trazado la perspectiva caballera de un tetraedro apoyado por su cara ABC en el triedro XOY, según los parámetros establecidos.
Conocemos las proyecciones diédricas del poliedro. Te pedimos que apliques los contenidos y procedimientos adquiridos hasta ahora para trazar la perspectiva caballera mediante las herramientas de dibujo tradicionales. |