2.1. Tetraedro
Para resolver la sección de un plano sobre un tetraedro aplicaremos el segundo método explicado en el apartado anterior.
Para ello contendremos cada arista del poliedro en un plano proyectante; además, podemos emplear homología para simplificar el trazado.
En el vídeo superior puedes ver la representación tridimensional de la sección, y su verdadera magnitud, que produce un plano proyectante vertical sobre una pirámide regular de base hexagonal, su similitud con el tetraedro nos sirve de ejemplo.
Seccionado por un plano proyectante vertical.
Cuando un plano proyectante secciona a una superficie la sección queda determinada directamente en la proyección correspondiente, esto es:- Si el plano secante es proyectante vertical la sección se muestra de manera directa en la proyección vertical.
- Si el plano secante es proyectante horizontal la sección queda determinada directamente en la proyección horizontal.
En la siguiente animación te mostramos como se obtiene las proyecciones de la sección producida por un plano proyectante vertical sobre un tetraedro.
Seccionado por un plano oblicuo.
Si el plano secante es oblicuo podemos obtener las proyecciones de la sección aplicando los métodos segundo y tercero explicados en el apartado anterior.En la animación inferior puedes ver cómo hemos empleado ambos métodos para obtener la sección de un plano secante sobre un tetraedro.
|
|
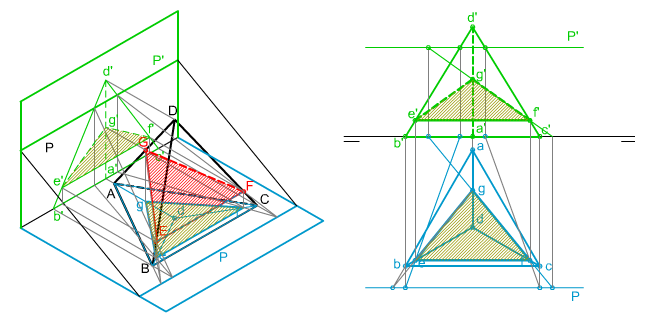
| En la imagen superior te mostramos cómo se ha determinado la sección plana producida por un plano paralelo a la LT en un Tetraedro ABCD.
Conocemos las proyecciones diédricas del Tetraedro y del plano. Te pedimos que apliques los contenidos y procedimientos adquiridos hasta ahora para determinar la sección plana mediante las herramientas de dibujo tradicionales. |