3.2. Diédrico
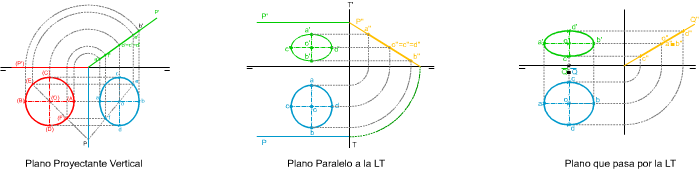
Las proyecciones de una circunferencia en el sistema diédrico dependerán de la posición que ocupe el plano que contenga dicha curva respecto de los planos de proyección.
En la imagen superior puedes ver varios ejemplos de proyección de una circunferencia contenida en un plano proyectante vertical (de canto), paralelo a la línea de tierra y que pase por ella.
Proyecciones de una circunferencia contenida en un plano oblicuo.
Como el plano no es ni paralelo ni perpendicular a los planos de proyección, la circunferencia se proyectará sobre ellos como Elipse, siendo sus ejes rectas paralelas a los planos de proyección (horizontal y frontal) y de máxima pendiente e inclinación
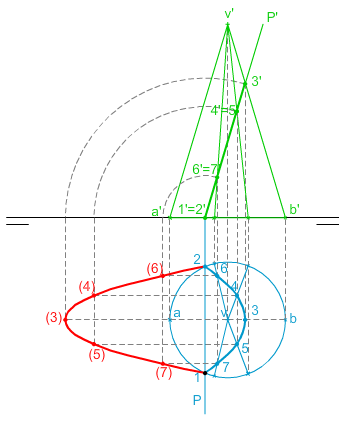
Sección del cono: parábola.
 Ya hemos visto como al seccionar un cono recto de revolución podemos obtener varias curvas cónicas.
Ya hemos visto como al seccionar un cono recto de revolución podemos obtener varias curvas cónicas.
En este caso particular hemos cortado el cono mediante un plano paralelo a una de sus generatrices lógicamente obtenemos una parábola, para determinar su proyección, en este caso horizontal, podemos recurrir al método de intersección de rectas, explicado en el apartado 2.3.