1.1. Definición y elementos
DEFINICIÓN:
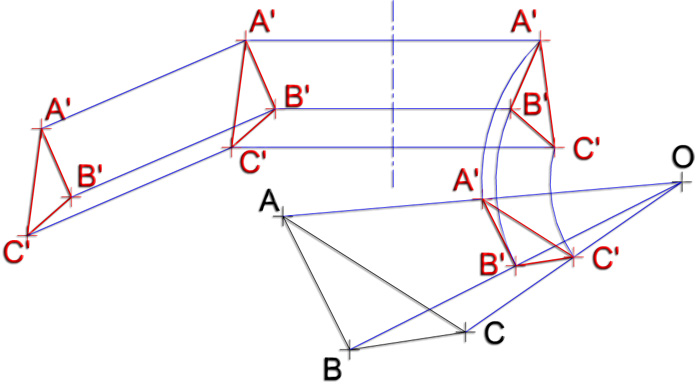
Una transformación geométrica es una operación o la combinación de varias de ellas, en que se parte de una forma original para generar otra nueva (transformada).
El resultado es un cambio (de posición, de tamaño, de forma, …) producido en una figura dada F cuando pasa a ser F’. A cada punto de la figura origen (F) se le hace corresponder en el mismo plano, otro de la forma transformada (F'). Las correspondencias entre los elementos de F y de F’ originan los diferentes tipos de transformaciones. La relación que exista entre los elementos origen y transformados debe de ser biunívoca.
ELEMENTOS:
En toda transformación existen tres elementos:
- Elementos característicos: Los que definen todas las correspondencias entre la figura original y la transformada.
- Elementos dobles: Los que se transforman en sí mismos.
- Elementos impropios: o en el infinito, pueden ser:
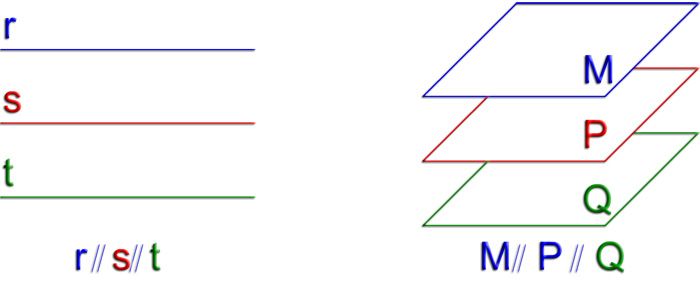
- Punto impropio: elemento común que tiene entre sí todas las rectas paralelas de un conjunto. Cualquier recta tiene un único punto impropio.
- Recta impropia: el elemento común que tienen entre sí todos los planos paralelos de un conjunto. Cualquier plano tiene una única recta impropia
- Plano impropio: es el lugar geométrico constituido por todos los elementos impropios de la geometría euclídea. Existe un único plano impropio y todo aquel elemento que no esté incluido en él es propio.
- Unívoca: A cada elemento de una de ellas le corresponde otro de la segunda, pero no se verifica la recíproca.
- Biunívoca: A cada elemento de la primera figura le corresponde otro de la segunda y a cada elemento de ésta otro de la primera
FIGURAS GEOMÉTRICAS. Se establecen tres categorías: de primera, de segunda y de tercera categoría.